MCC | 机器学习中优于F1-score和accuracy的一个性能评价指标

在机器学习中，模型性能的评估是一个关键问题。常见的评价指标有F1-score, Accuracy, Precision, Recall, ROC 和 AUC (对这些评价指标不了解的，可以参考生信菜鸟团之前的一篇文章: 机器学习实战 | 机器学习性能指标 )。但是我们对这些统计指标的可靠性要保持谨慎的态度，特别是在不平衡的数据集上。

F1-score, Accuracy, Precision, Recall

例如，在一个二元分类模型中，我们的数据是宠物图像，每张图片可以是狗🐶或猫🐱，分类器在每张照片中检测到一只宠物，然后我们测量其性能。假如我们总共有24张图片，然后分类器检测的混淆矩阵如下：

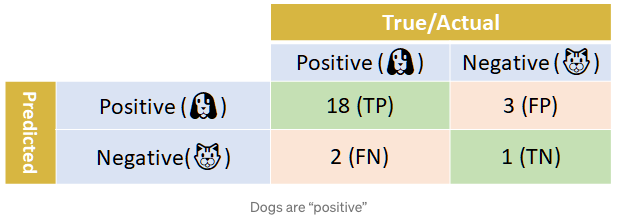
我们依次计算下Precision, Recall, F1 score。

Precision = TP/(TP+FP) = 18/(18+3) = 0.86

Recall = TP/(TP+FN) = 18/(18+2) = 0.90

F1 = 2 * (Precision*Recall/Precision+Recall) = 0.88

从以上这些指标的计算结果来看，我们的模型似乎还不错。但是关于猫 (negative class)的分类，只有1个是正确识别了。那为什么F1-score的值还这么高呢？

从计算公式中，我们可以看出来，无论是Precision, Recall还是F1 score，他们都只关注了一个类别，即positive class。TN完全没有考虑。

如果我们设定数据中猫是Positive class，那么我们的混淆矩阵可以转换为：

Precision = TP/(TP+FP) = 1/(1+2) = 0.33

Recall = TP/(TP+FN) = 1/(1+3) = 0.25

F1 = 2 * (Precision*Recall/Precision+Recall) = 0.29

从这里的计算结果可以发现，这个分类器对猫的识别很差。

然后我们再看下Accuracy，

1	Accuracy = TP+TN/(TP+TN+FP+FN) = 19/24=0.79

这个结果是相当有误导性的，因为虽然 90% (18/20)的狗被准确分类，但猫只有 25% (1/4)。如果取平均值，结果也只有57.5%，也是低于79%的。这里的原因是因为数据中两个分类的类别是不平衡的。

从以上计算中可以知道Accuracy对类别不平衡很敏感；Precision, Recall和 F1 score是不对称的，只关注了一个类别。

Matthews correlation coefficient，MCC

马修斯相关系数（MCC）是phi系数（φ）的一个特例。即将True Class和Predicted Class视为两个（二进制）变量，并计算它们的相关系数（与计算任何两个变量之间的相关系数类似）。真实值和预测值之间的相关性越高，预测效果越好。只有当预测在所有四个混淆矩阵类别（TP、TN、FN和FP）中都获得了良好的结果时，它才会产生高分。

计算公式如下：

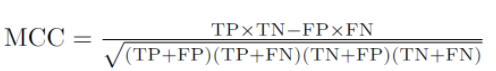
根据计算公式，可知当分类器是完美的（FP = FN = 0），MCC的值是1，表示完全正相关。相反，当分类器总是分类错误时（TP = TN = 0），得到的数值是-1，代表完美的负相关。所以，MCC的值总是在-1和1之间，0意味着分类器不比随机二分类选择好。此外，MCC是完全对称的，所以没有哪个类别比其他类别更重要，如果把正反两个类别换一下，仍然会得到相同的值。

然后我们再计算一下，上面例举的数据中MCC的值：

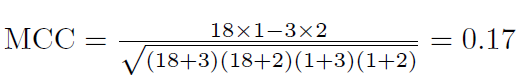
MCC的值是0.17 ，表明预测类和真实类是弱相关的。从以上的计算和分析，我们知道这种弱相关是因为分类器不擅长对猫进行分类。

在python中，scikit-learn模块包含MCC计算的函数

sklearn.metrics.matthews_corrcoef(y_true, y_pred, *, sample_weight=None)

from sklearn.metrics import matthews_corrcoef
y_true = [+1, +1, +1, -1]
y_pred = [+1, -1, +1, +1]
matthews_corrcoef(y_true, y_pred)
-0.33...

F1-score, Accuracy, Precision, Recall

Matthews correlation coefficient，MCC

参考资料