卷积神经网络入门

卷积神经网络(CNN)简介

卷积神经网络即Convolutional Neural Networks (CNN or COnvNet) 是一种自动化提取特征的深度学习模型。这是一种深度的前馈人工神经网络（ feed-forward artificial neural network），前馈神经网络也称作多层感知机（multi-layer perceptrons，MLPs）。

CNNs是受生物视觉皮层的启发。视觉皮层有一些小区域的细胞，它们对视野的特定区域很敏感。这个想法是由Hubel和Wiesel在1962年做的一个的实验扩展了这个想法。在这个实验中，研究人员表明，大脑中的一些个别神经元只有在出现垂直或水平边缘等特定方向的边缘时才会激活或发射。但是在2012年，Alex Krizhevsky利用卷积神经网络赢得了当年的ImageNet大赛，将分类误差从26%降到15%，之后CNNs再一次火爆。

CNNs如今在多个领域都展现出巨大的应用潜能。如：

图像识别，目标检测，分割，人脸识别
自动驾驶汽车等

卷积神经网络(CNN)的结构单元

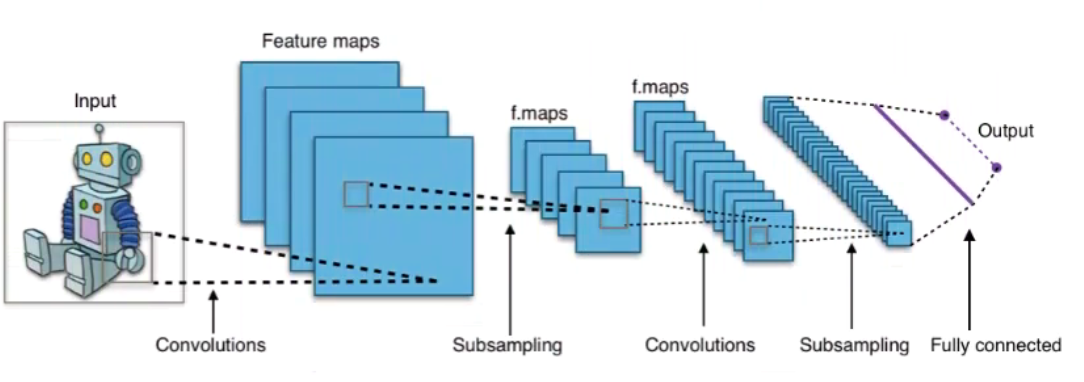
输入层(input layer)

卷积层（convolution layer)

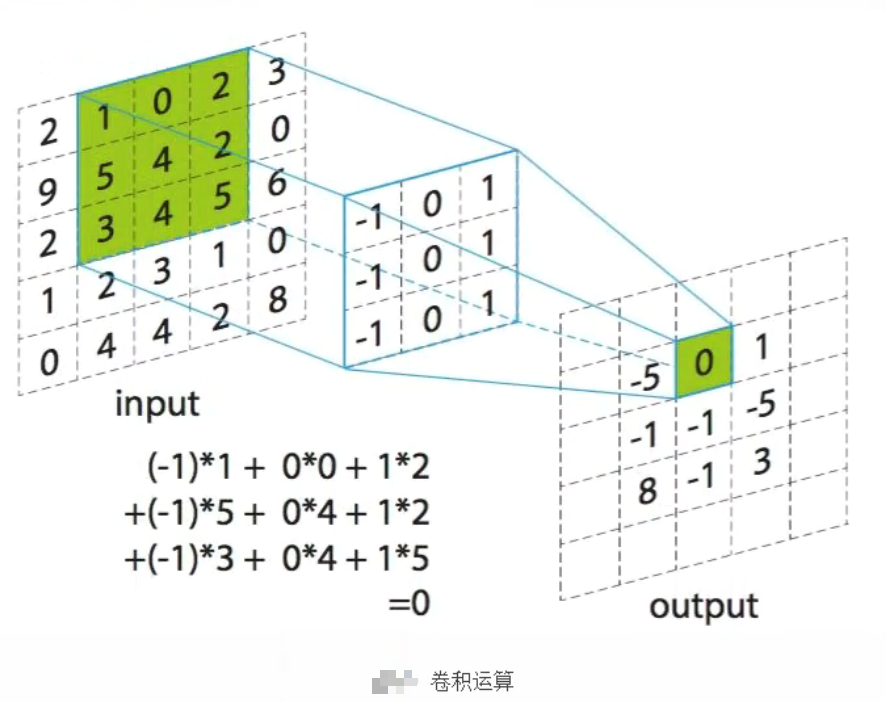
权值共享。我们通过卷积核与输入进行卷积运算。通过下图可以理解如何进行卷积运算。卷积核从左到右对输入进行扫描，每次滑动1格（步长为1），下图为滑动一次后，卷积核每个元素和输入中绿色框相应位置的元素相乘后累加，得到输出中绿色框中的0。一般会使用多个卷积核对输入数据进行卷积，得到多个特征图

激活层

对卷积层的输出进行一个非线性映射，因为卷积计算是一种线性计算。常见的激活函数有relu、tanh、sigmoid等，一般使用relu。使用relu的原因是在反向传播计算梯度中，使用relu求导明显会比tanh和sigmoid简单，可以减少计算量

池化层(subsampling/pooling layer)

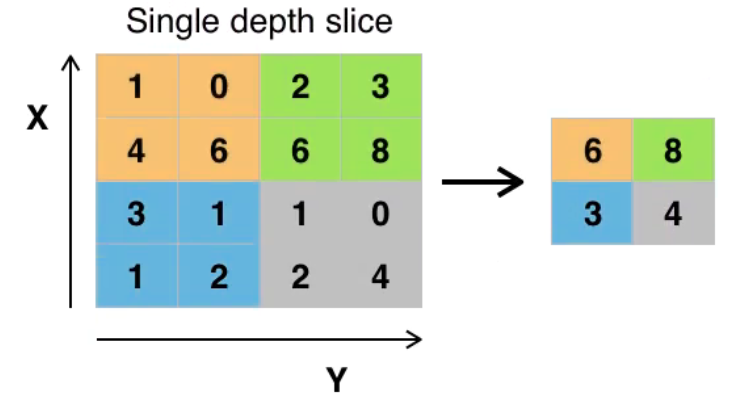
池化的目的就是减少特征图的维度，减少数据的运算量。池化层是在卷积层之后，对卷积的输出，进行池化运算。池化运算，一般有两种MaxPooling和MeanPooling。

全连接层(Fully connected layer)

主要是对特征进行重新的拟合，减少特征信息的丢失。通过卷积池化操作后得到的是多个特征矩阵，而全连接层的输入为向量，所以在进行全连接层之前，要将多个特征矩阵“压平”为一个向量。

输出层(output layer)

卷积神经网络(CNN)代码示例

这里介绍以Keras实现CNN的代码示例

数据集介绍

Fashion-MNIST数据集是Zalando的文章图像数据集，包含来自10个类别的70000个时尚产品的28x28灰度图像，每个类别有7000个图像。训练集有60000张图片，测试集有10000张图片。

数据载入

首先载入Keras模块，其是基于tensorflow框架的

# install tensorflow
pip install tensorflow
pip install keras
from keras.datasets import fashion_mnist
(train_X,train_Y), (test_X,test_Y) = fashion_mnist.load_data()

调整像素和图像大小

import numpy as np
from keras.utils import to_categorical
import matplotlib.pyplot as plt

print('Training data shape : ', train_X.shape, train_Y.shape)

print('Testing data shape : ', test_X.shape, test_Y.shape)

# Find the unique numbers from the train labels
classes = np.unique(train_Y)
nClasses = len(classes)
print('Total number of outputs : ', nClasses)
print('Output classes : ', classes)

可以看出输出的类别共包括10（0-9）类

查看数据集中图像

plt.figure(figsize=[5,5])

# Display the first image in training data
plt.subplot(121)
plt.imshow(train_X[0,:,:], cmap='gray')
plt.title("Ground Truth : {}".format(train_Y[0]))

# Display the first image in testing data
plt.subplot(122)
plt.imshow(test_X[0,:,:], cmap='gray')
plt.title("Ground Truth : {}".format(test_Y[0]))

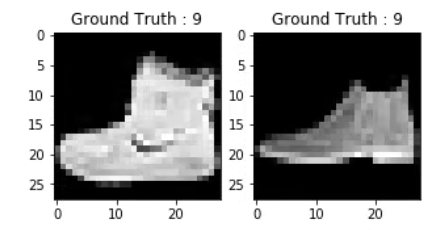
上面两个图的输出看起来像一个短靴，这个类被分配了一个类标签9。同样的，其他的时尚产品会有不同的标签，但是相似的产品会有相同的标签。这意味着所有7000张短靴图片的类别标签都是9。

数据前处理

上面的图像可以看出是灰度图像，像素值的范围再0-255,且图像的维度为28*28.

Step1: 首先将训练数据和测试数据的2828图像转化为2828*1的矩阵

1
2
3

train_X = train_X.reshape(-1, 28,28, 1)
test_X = test_X.reshape(-1, 28,28, 1)
train_X.shape, test_X.shape

Step2: 现在的数据是int8格式的，因此在将其输入网络之前，需要将其类型转换为float32，还必须重新调整范围为0 - 1(包括1)的像素值。

train_X = train_X.astype('float32')
test_X = test_X.astype('float32')
train_X = train_X / 255.
test_X = test_X / 255.

Step3: 将类标签转换为一个热编码向量

机器学习算法不能直接处理分类数据, 故需将分类数据转换为数字向量

# Change the labels from categorical to one-hot encoding
train_Y_one_hot = to_categorical(train_Y)
test_Y_one_hot = to_categorical(test_Y)

# Display the change for category label using one-hot encoding
print('Original label:', train_Y[0])
print('After conversion to one-hot:', train_Y_one_hot[0])

拆分训练数据和测试数据集

from sklearn.model_selection import train_test_split
train_X,valid_X,train_label,valid_label = train_test_split(train_X, train_Y_one_hot, test_size=0.2, random_state=13)
# check the shape of training and validation set
train_X.shape,valid_X.shape,train_label.shape,valid_label.shape

网络

图像的大小是28 x 28。前面将图像矩阵转换为数组，在0和1之间重新调整大小，重塑它的大小为28 x 28 x 28 x 1，然后将其作为网络的输入。

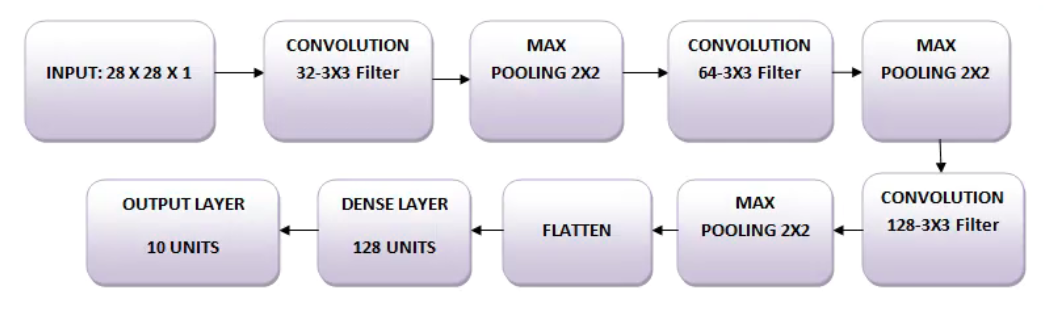
下面将使用三个卷积层。

第一层将有32-3×3个滤波器。

第二层将有64-3×3滤波器和

第三层将有128-3×3个滤镜。

此外，还有3个最大pooling层，每个层的大小为2×2。

创建模型

import keras
from keras.models import Sequential,Input,Model
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras.layers.normalization import BatchNormalization
from keras.layers.advanced_activations import LeakyReLU

这里使用64的批处理量，也可以使用128或256的批处理量，这一切都取决于内存。它对确定学习参数的贡献很大，并影响到预测的准确性。你将训练网络的20个时程

1
2
3

batch_size = 64
epochs = 20
num_classes = 10

神经网络架构

在Keras中，可以通过逐一添加所需的图层来堆叠图层。首先用Conv2D()添加第一个卷积层。注意，之所以使用这个函数，是因为在处理图像。接下来，添加Leaky ReLU激活函数，它可以帮助网络学习非线性决策边界。因为这里的例子有十个不同的类，需要一个非线性决策边界，可以将这十个不能线性分离的类分开。

更具体地说，添加了Leaky ReLU，因为它们试图修复垂死的整流线性单元（ReLU）问题。ReLU 激活函数在神经网络架构中被大量使用，在卷积网络中，ReLU 激活函数被证明比广泛使用的对数 sigmoid 函数更有效。截止到2017年，这种激活函数是深度神经网络中最流行的一种激活函数。ReLU函数允许将激活函数的阈值设定为零。然而，在训练过程中，ReLU单元可能会 “死亡”。当一个大的梯度流过ReLU神经元时，就会发生这种情况：它可能会导致权重以这样的方式更新，以至于神经元再也不会在任何数据点上激活。如果这种情况发生，那么流经该单元的梯度将永远为零。泄漏的ReLU试图解决这个问题：函数不会为零，而是有一个小的负斜率。

接下来，用MaxPooling2D()等添加最大池化层。最后一层是Dense层，它有一个软MAX的激活函数，有10个单位，这对于这个多类分类问题是需要的。

fashion_model = Sequential()
fashion_model.add(Conv2D(32, kernel_size=(3, 3),activation='linear',input_shape=(28,28,1),padding='same'))
fashion_model.add(LeakyReLU(alpha=0.1))
fashion_model.add(MaxPooling2D((2, 2),padding='same'))
fashion_model.add(Conv2D(64, (3, 3), activation='linear',padding='same'))
fashion_model.add(LeakyReLU(alpha=0.1))
fashion_model.add(MaxPooling2D(pool_size=(2, 2),padding='same'))
fashion_model.add(Conv2D(128, (3, 3), activation='linear',padding='same'))
fashion_model.add(LeakyReLU(alpha=0.1))                  
fashion_model.add(MaxPooling2D(pool_size=(2, 2),padding='same'))
fashion_model.add(Flatten())
fashion_model.add(Dense(128, activation='linear'))
fashion_model.add(LeakyReLU(alpha=0.1))                  
fashion_model.add(Dense(num_classes, activation='softmax'))

编译模型

使用Adam optimizer

1	fashion_model.compile(loss=keras.losses.categorical_crossentropy, optimizer=keras.optimizers.Adam(),metrics=['accuracy'])

使用summary函数来可视化在上述步骤中创建的层。这将显示每个层中的一些参数(权重和偏差)以及模型中的总参数。

1	fashion_model.summary()

训练模型

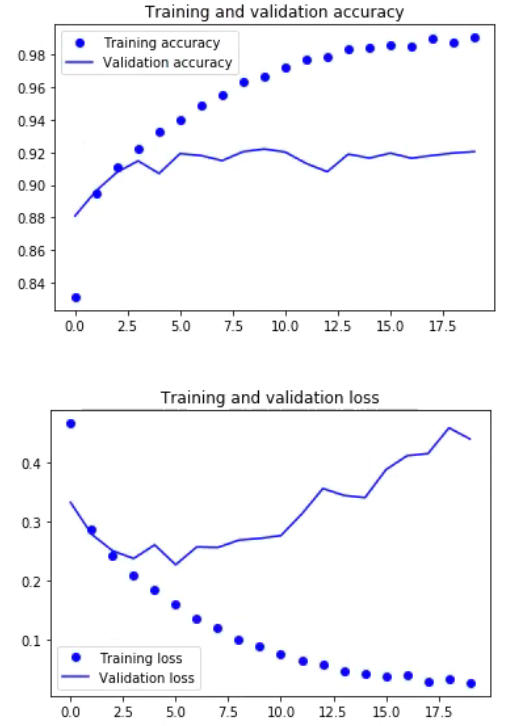
使用Keras的fit()函数训练模型，该模型训练了20个 epochs。fit()函数将返回一个历史对象；通过在fashion_train中讲述这个函数的结果，你可以在以后用它来绘制训练和验证之间的精度和损失函数图，这将帮助你直观地分析你的模型的性能。

1	fashion_train = fashion_model.fit(train_X, train_label, batch_size=batch_size,epochs=epochs,verbose=1,validation_data=(valid_X, valid_label))

模型评估

1
2
3

test_eval = fashion_model.evaluate(test_X, test_Y_one_hot, verbose=0)
print('Test loss:', test_eval[0])
print('Test accuracy:', test_eval[1])

可视化

accuracy = fashion_train.history['acc']
val_accuracy = fashion_train.history['val_acc']
loss = fashion_train.history['loss']
val_loss = fashion_train.history['val_loss']
epochs = range(len(accuracy))
plt.plot(epochs, accuracy, 'bo', label='Training accuracy')
plt.plot(epochs, val_accuracy, 'b', label='Validation accuracy')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()

参考资料

CNN讲解及实践

CNN（卷积神经网络）

Convolutional Neural Networks in Python with Keras

Convolutional Neural Networks for Beginners using Keras and TensorFlow

深度学习